티스토리 뷰
트리(Tree)
- 그래프의 일종으로, 여러 노드가 한 노드를 가리킬 수 없는 구조이다.
- 간단하게 회로가 없고, 서로 다른 두 노드를 잇는 길이 하나뿐인 그래프를 트리라고 부른다.
- 트리에서 최상위 노드를 루트노드(root node)라고 한다.
- 한 노드 A가 노드 B를 가리킬 때 A를 B의 부모노드(parent node), B를 A의 자식노드(chiled node)라고 한다.
- 자식 노드가 없는 노드를 잎 노드(leaf node)라고 한다.
- 잎 노드가 아닌 노드를 내부 노드(internal node)라고 한다.
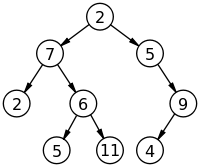
출처 : 위키백과
트리의 기본적인 성질
- 노드가 N개인 트리는 항상 N-1개의 링크(link)를 가진다.
- 트리에서 루트에서 어떤 노드로 가는 경로는 유일하다. 또한 임의의 두 노드간의 경로도 유일하다.
(같은 노드를 두 번 이상 방문하지 않는다는 조건하에)
이진 트리(Binary Tree)
- 노드가 최대 두 개의 자식 노드를 가지는 트리를 뜻한다.
- 보통 첫 번쨰 노드를 부모 노드라고 하며 자식 노드는 왼쪽(left)와 오른쪽(right)으로 불린다.
- 이진 탐색 트리와 이진 힙의 구현에 흔히 쓰인다.

출처 : 위키백과
이진 트리 응용의 예 :
① Expression Tree(수식 트리)
② Huffman Code
③ Full and Complete Binary Tree
- Full Binary Tree(정 이진 트리)는 단말 노드가 아닌 모든 노드가 2개의 자식을 가진 트리이다.
- Complete Binary Tree(완전 이진 트리)는 끝 부분(마지막 레벨)을 제외하고 모든 노드가 채워진 이진 트리이다.
마지막 레벨의 노드들은 왼쪽으로 채워져 있다. 마지막 레벨이 다 채워질 수도 있다.

이진 트리의 순회(traversal)
순회 : 이진 트리의 모든 노드를 방문하는 일
In-order(중순위) 순회 : 왼쪽 자식 노드, 내 노드, 오른쪽 자식 노드 순서로 방문한다.
의사코드
IN-ORDER-TREE-WALK(x){ if x != NIL then IN-ORDER-TREE-WALK(left[x]) print key[x] IN-ORDER-TREE-WALK(right[x]) }
Pre-order(선순위) 순회 : 내 노드, 왼쪽 자식 노드, 오른쪽 자식 노드 순서로 방문한다.
PRE-ORDER-TREE-WALK(x){ if x != NIL then print key[x] PRE-ORDER-TREE-WALK(left[x]) PRE-ORDER-TREE-WALK(right[x]) }
Post-order(후순위) 순회 : 왼쪽 자식 노드, 오른쪽 자식 노드, 내 노드 순서로 방문한다.
POST-ORDER-TREE-WALK(x){ if x != NIL then POST-ORDER-TREE-WALK(left[x]) POST-ORDER-TREE-WALK(right[x]) print key[x] }
Lever-order(레벨 오더) 순회 : 내 노드, 내 노드로 부터 깊이 1인 노드들, ... , 내 노드로 부터 깊이 N인 노드들
LEVEL-ORDER-TREE-TRAVERSAL(){
visit the root;
Q <- root;
while Q is not empty do
V <- dequeue(Q);
visit children of V;
enqueue children of v into Q;
end.
end.
}'알고리즘' 카테고리의 다른 글
| Hashing(해싱) (0) | 2017.12.17 |
|---|---|
| BST : Binary Search Tree(이진 검색 트리) (0) | 2017.12.17 |
| 객체의 정렬 : Comparable, Comparator (0) | 2017.12.12 |
| 정렬 알고리즘 비교 (0) | 2017.12.12 |
| Radix Sort(기수 정렬) (1) | 2017.12.12 |

